المعادلات التفاضلية الجزئية – لقد حل الذكاء الاصطناعي لغزًا رياضيًا رئيسيًا لفهم عالمنا

يمكن أن تصف المعادلات التفاضلية الجزئية كل شيء من حركة الكواكب إلى حركة الصفائح في تركيبة الأرض، ولكن من المعروف أن حلها صعب. بعد سنوات من التأمل فيها في المرحلة الجامعية أثناء دراسة الهندسة الميكانيكية ، لم أستخدمها مطلقًا منذ ذلك الحين في العالم الحقيقي. كتبت كارن على موقع ام اي تي.

المعادلات التفاضلية الجزئية

لكن المعادلات التفاضلية الجزئية، هي أيضًا نوع من السحر. حيث إنها فئة من المعادلات الرياضية التي تعتبر جيدة حقًا في وصف التغيير عبر المكان والزمان. وبالتالي فهي مفيدة جدًا لوصف الظواهر الفيزيائية في كوننا. يمكن استخدامها لنمذجة كل شيء من مدارات الكواكب إلى الصفائح الأرضية إلى اضطراب الهواء الذي يزعج الرحلة، والذي بدوره يسمح لنا بالقيام بأشياء عملية مثل التنبؤ بالنشاط الزلزالي وتصميم طائرات آمنة.

وصف حركة أي سائل

المشكلة هي أن معادلات التفاضل الجزئية يصعب حلها. وهنا، ربما يكون أفضل توضيح لمعنى حل هو طرح مثال. لنفترض أنك تحاول محاكاة الاضطرابات الجوية لاختبار تصميم جديد للطائرة. هناك معادلات معروفة تسمى Navier-Stokes تستخدم لوصف حركة أي سائل. يتيح لك حل هذه المعادلة التقاط لقطة لحركة الهواء (مثل ظروف الرياح) في أي وقت وتحديد كيفية استمراره في الحركة، أو كيف كان يتحرك من قبل.

هذه الحسابات معقدة للغاية ومكثفة من الناحية الحسابية، وهذا هو السبب في أن التخصصات التي تستخدم الكثير من معادلات التفاضل الجزئية غالبًا ما تعتمد على أجهزة الكمبيوتر العملاقة لإجراء العمليات الحسابية. وهذا هو سبب اهتمام مجال الذكاء الاصطناعي بهذه المعادلات بشكل خاص. إذا تمكنا من استخدام التعلم العميق لتسريع عملية حلها، فيمكن أن يكون مفيدًا جدًا للبحث العلمي والهندسة.

تقنية جديدة للتعلم العميق لحل المعادلات التفاضلية الجزئية

قدم باحثون في معهد كاليفورنيا للتقنية الآن تقنية جديدة للتعلم العميق لحل المعادلات التفاضلية الجزئية التي تعد أكثر دقة بشكل كبير من طرق التعلم العميق التي تم تطويرها سابقًا. كما أنه أكثر قابلية للتعميم، وهو قادر على حل عائلات كاملة من المعادلات. مثل معادلة Navier-Stokes لأي نوع من السوائل – دون الحاجة إلى إعادة التدريب. أخيرًا، إنه أسرع بألف مرة من الصيغ الرياضية التقليدية، مما يخفف من اعتمادنا على أجهزة الكمبيوتر العملاقة ويزيد قدرتنا الحسابية على نمذجة مشاكل أكبر.

عندما تناسب الوظيفة

أول شيء يجب فهمه هنا هو أن الشبكات العصبية هي في الأساس مقربات وظيفية. عندما يتدربون أي الشبكات العصبية، على مجموعة بيانات من المدخلات والمخرجات المزدوجة. فإنهم في الواقع يحسبون الوظيفة، أو سلسلة العمليات الحسابية، التي ستنقل إحداها إلى الأخرى. فكر في بناء نموذج لكشف القطط. أنت تدرب الشبكة العصبية عن طريق تزويدها بالكثير من صور القطط و الأشياء التي ليست قطط (المدخلات). وتسمية كل مجموعة بـ 1 أو 0 ، على التوالي (المخرجات). تبحث الشبكة العصبية بعد ذلك عن أفضل وظيفة يمكنها تحويل كل صورة قطة إلى 1 وكل صورة لكل شيء آخر إلى 0. وبهذه الطريقة يمكن أن تنظر إلى صورة جديدة وتخبرك ما إذا كانت قطة أم لا. إنها تستخدم الوظيفة التي وجدتها لحساب إجابتها. وإذا كان تدريبها جيدًا، فستحصل عليها بشكل صحيح في معظم الأوقات.

نحن نحاول في النهاية العثور على وظيفة تصف، على سبيل المثال، حركة جسيمات الهواء عبر الفضاء والزمان الماديين.

الآن هذا هو جوهر الورقة. عادة ما يتم تدريب الشبكات العصبية لتقريب الوظائف بين المدخلات والمخرجات المحددة في الفضاء الإقليدي، الرسم البياني الكلاسيكي الخاص بك باستخدام محاور x و y و z. لكن هذه المرة، قرر الباحثون تحديد المدخلات والمخرجات في فضاء فورير. وهو نوع خاص من الرسم البياني لرسم ترددات الموجة، اي يعتمد على التردد بدلاً من الزمن.

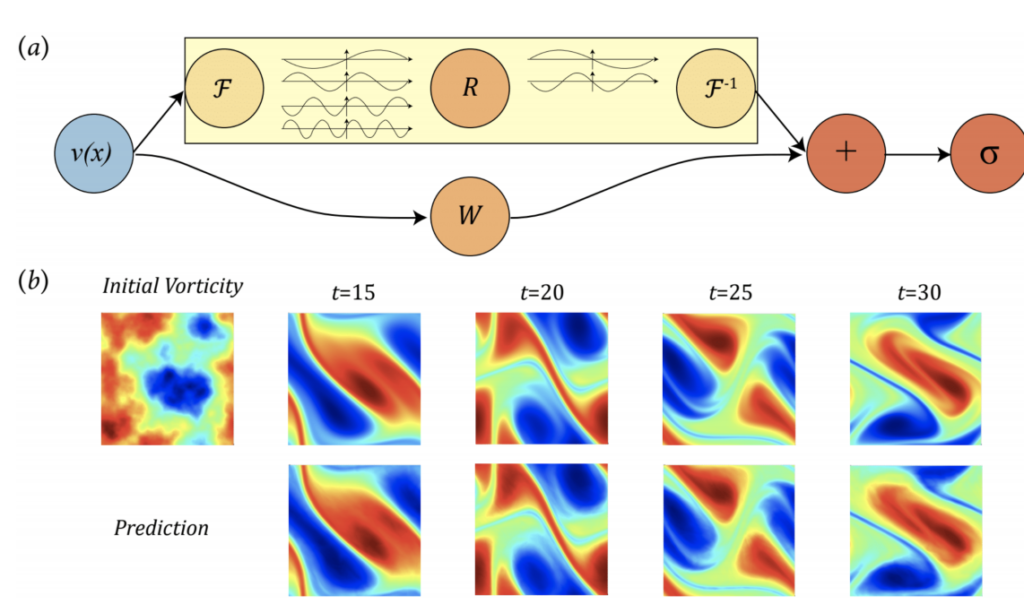
تقول أنيما، أستاذة معهد كاليفورنيا للتكنولوجيا والتي أشرفت على البحث جنبًا إلى جنب مع زملائها، الأستاذين أندرو ستيوارت وكاوشيك. إن الحدس الذي استفادوا منه من العمل في مجالات أخرى هو أنه يمكن وصف شيء مثل حركة الهواء على أنه مزيج من ترددات الموجات. الاتجاه العام للرياح على المستوى الكلي يشبه التردد المنخفض مع موجات طويلة جدًا وخاملة، في حين أن الدوامات الصغيرة التي تتشكل على المستوى الجزئي تشبه الترددات العالية ذات الترددات القصيرة جدًا والسريعة.

الكفاءة بالإضافة إلى السرعة الهائلة

لماذا هذا مهم؟ لأنه من الأسهل بكثير تقريب دالة فورير في مساحة فورير بدلاً من الخوض مع أالمعادلات التفاضلية الجزئية في الفضاء الإقليدي، مما يبسط عمل الشبكة العصبية إلى حد كبير. حدد مكاسب الدقة والكفاءة الرئيسية: بالإضافة إلى ميزة السرعة الهائلة التي تتمتع بها على الطرق التقليدية، فإن أسلوبهم يحقق معدل خطأ أقل بنسبة 30٪ عند حل Navier-Stokes مقارنة بأساليب التعلم العميق السابقة.

قابلية للتعميم

الأمر برمته ذكي للغاية، كما أنه يجعل الطريقة أكثر قابلية للتعميم. كان لابد من تدريب أساليب التعلم العميق السابقة بشكل منفصل لكل نوع من السوائل، في حين أن هذه الطريقة تحتاج فقط إلى التدريب مرة واحدة للتعامل معها جميعًا، كما أكدت ذلك تجارب الباحثين. على الرغم من أنهم لم يحاولوا بعد توسيع هذا ليشمل أمثلة أخرى، إلا أنه ينبغي أيضًا أن يكون قادرًا على التعامل مع كل تكوين للأرض عند حل المعادلات المتعلقة بالنشاط الزلزالي. أو كل نوع من المواد عند حل المعادلات المتعلقة بالتوصيل الحراري.

محاكاة فائقة

لم يقم الأساتذة وطلاب الدكتوراه بإجراء هذا البحث فقط من أجل المتعة النظرية منه. يريدون جلب الذكاء الاصطناعي إلى المزيد من التخصصات العلمية. من خلال التحدث إلى العديد من المتعاونين في علوم المناخ وعلم الزلازل وعلوم المواد. قررت أناندكومار أولاً مواجهة تحدي المعادلات التفاضلية الجزئية مع زملائها وطلابها. إنهم يعملون الآن على وضع طريقتهم موضع التنفيذ مع باحثين آخرين في معهد كاليفورنيا للتكنولوجيا ومختبر لورانس بيركلي الوطني.